In [1]:
%%HTML
<link rel="stylesheet" type="text/css" href="https://raw.githubusercontent.com/malkaguillot/Foundations-in-Data-Science-and-Machine-Learning/refs/heads/main/docs/utils/custom.css">
<link rel="stylesheet" type="text/css" href="../utils/custom.css">

Foundations in Data Science and Machine Learning¶

Module 5a: Machine Learning - Regression¶

Malka Guillot¶

HSG Logo

References¶

  • Békés & Kézdi (2022) 13 & 14
  • Introduction to Statistical Learning chap 1. & 2 & 5.1
  • Kleinberg, Ludwig, Mullainathan, and Obermeyer (2015), "Prediction Policy Problems." American Economic Review, 105 (5), pp. 491-95.
  • Mullainathan and Spiess (2017), "Machine Learning: An Applied Econometric Approach"), Journal of Economic Perspectives, 31 (2), pp. 87-106,

What is ML?¶

A concise definition by Athey (2018):

"...[M]achine learning is a field that develops algorithms designed to be applied to datasets, with the main areas of focus being prediction (regression), classification, and clustering or grouping tasks."

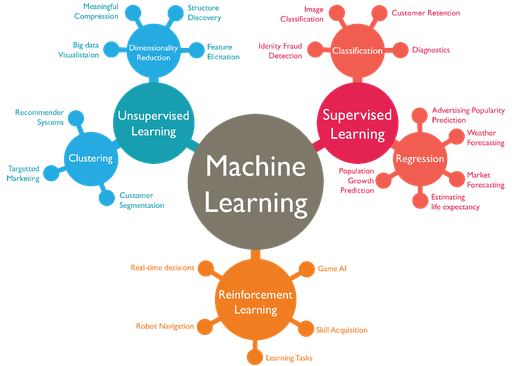
Specifically, there are three broad classifications of ML problems:

  • supervised learning.
  • unsupervised learning.
  • reinforcement learning.

Most of the hype you hear about in recent years relates to supervised learning, and in particular, deep learning.

ML Landscape¶

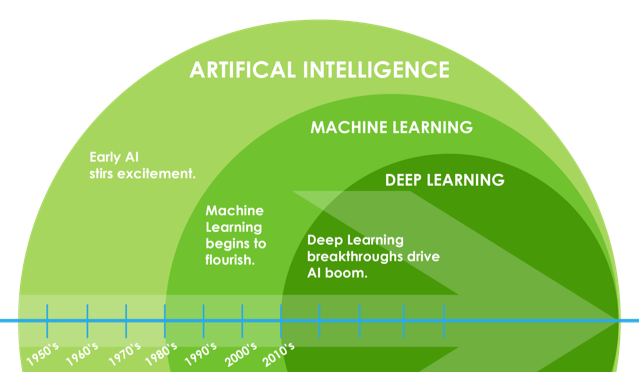
No description has been provided for this image

An Aside: ML and Artificial Intelligence (AI)¶

No description has been provided for this image

Unsupervised Learning¶

In unsupervised learning, the goal is to divide high-dimensional data into clusters that are similar in their set of features $(X)$.

Examples of algorithms:

  • principal component analysis (PCA)
  • $k$-means clustering
  • Latent Dirichlet Allocation (LDA)

Applications:

  • image recognition
  • cluster analysis
  • topic modelling

Example: Clustering OECD Inflation Rates¶

No description has been provided for this image

Source: Baudot-Trajtenberg and Caspi (2018)

Reinforcement Learning (RL)¶

A definition by Sutton and Barto (2018):

_"Reinforcement learning is learning what to do—how to map situations to actions—so as to maximize a numerical reward signal. The learner is not told which actions to take, but instead must discover which actions yield the most reward by trying them."_

Prominent examples:

  • Games (e.g., Chess, AlphaGo).

  • Autonomous cars.

Supervised Learning¶

Consider the following data generating process (DGP):

$$Y=f(\boldsymbol{X})+\epsilon$$ where $Y$ is the outcome variable, $\boldsymbol{X}$ is a $1\times p$ vector of "features", and $\epsilon$ is the irreducible error.

  • Training set ("in-sample"): $\\{(x_i,y_i)\\}_{i=1}^{n}$
  • Test set ("out-of-sample"): $\\{(x_i,y_i)\\}_{i=n+1}^{m}$
No description has been provided for this image

Typical assumptions: (1) independent observations; (2) stable DGP across training and test sets.

The Goal of Supervised Learning¶

Use a labelled test set ($X$ and $Y$ are known) to construct $\hat{f}(X)$ such that it generalizes to unseen test set (only $X$ is known).

  • If $Y$ is continuous: regression problem,

    • we are interested in estimating the conditional mean function $E[Y|X]$.
    • Example: Predicting house prices based on their features (e.g., size, location, number of bedrooms).

  • If $Y$ is categorical: classification problem,

    • we are interested in estimating the conditional probability function $P(Y|X)$.
    • Example: Predicting whether an email is spam or not based on its content.

Supervised Learning Algorithms¶

ML comes with a rich set of parametric and non-parametric prediction algorithms (approximate year of discovery in parenthesis):

  • Linear and logistic regression (1805, 1958).
  • Decision and regression trees (1984).
  • K-Nearest neighbors (1967).
  • Support vector machines (1990s).
  • Neural networks (1940s, 1970s, 1980s, 1990s).
  • Simulation methods (Random forests (2001), bagging (2001), boosting (1990)).
  • etc.

Supervised ML Workflow¶

  • Step 1: Define the Prediction Task
    • Pre-processing of the features
    • Decompose the observations in test/training set
  • Step 2: Explore the Data
  • Step 3: Choose the Model Cross-Validation Strategy
  • Step 4: Hyperparameter Tuning with Cross-Validationn
    • Assess the validity of the model
    • Select the best parameters
  • Step 5: Train the Final Model with Best Hyperparameters on the Train Set
  • Step 6: Evaluate the Model on the Holdout Test set
    • Training the best model on the training set and evaluate the model using the test set
  • Step 7: (Deploy the Model)

Step 1: Define the Prediction Task

¶

Boston housing data¶

We will use the Boston housing data: housing data for 506 census tracts of Boston from the 1970 census (Harrison and Rubinfeld, 1978).

The sample is available from sklearn and contains :

  • 13 attributes of housing markets around Boston population.
    • medv (target): median value of owner-occupied homes in USD 1000's.
    • lstat(predictor): percentage of lower status of the
    • chas (predictor): Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
  • 506 entries: aggregated data for homes from various suburbs in Boston, Massachusetts.

Objective: predict the value of prices medv of the house using the given features

Set up and load data¶

In [2]:
import numpy as np
import pandas as pd
# import patsy

from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.model_selection import GridSearchCV, KFold, train_test_split
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_curve, roc_auc_score, classification_report, accuracy_score, confusion_matrix 

import seaborn as sns
import matplotlib.pyplot as plt
In [3]:
df = pd.read_csv("../../data/BostonHousing.csv")

The data contain the following variables:

Variable Description
CRIM per capita crime rate by town
ZN proportion of residential land zoned for lots over 25,000 sq.ft.
INDUS proportion of non-retail business acres per town
CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
NOX nitric oxides concentration (parts per 10 million)
RM average number of rooms per dwelling
AGE proportion of owner-occupied units built prior to 1940
DIS weighted distances to five Boston employment centres
RAD index of accessibility to radial highways
TAX full-value property-tax rate per $10,000
PTRATIO pupil-teacher ratio by town
B 1000(Bk - 0.63)^2 where Bk is the proportion of black people by town
LSTAT % lower status of the population
In [4]:
df.describe()
Out[4]:
crim zn indus chas nox rm age dis rad tax ptratio b lstat medv
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean 3.613524 11.363636 11.136779 0.069170 0.554695 6.284634 68.574901 3.795043 9.549407 408.237154 18.455534 356.674032 12.653063 22.532806
std 8.601545 23.322453 6.860353 0.253994 0.115878 0.702617 28.148861 2.105710 8.707259 168.537116 2.164946 91.294864 7.141062 9.197104
min 0.006320 0.000000 0.460000 0.000000 0.385000 3.561000 2.900000 1.129600 1.000000 187.000000 12.600000 0.320000 1.730000 5.000000
25% 0.082045 0.000000 5.190000 0.000000 0.449000 5.885500 45.025000 2.100175 4.000000 279.000000 17.400000 375.377500 6.950000 17.025000
50% 0.256510 0.000000 9.690000 0.000000 0.538000 6.208500 77.500000 3.207450 5.000000 330.000000 19.050000 391.440000 11.360000 21.200000
75% 3.677083 12.500000 18.100000 0.000000 0.624000 6.623500 94.075000 5.188425 24.000000 666.000000 20.200000 396.225000 16.955000 25.000000
max 88.976200 100.000000 27.740000 1.000000 0.871000 8.780000 100.000000 12.126500 24.000000 711.000000 22.000000 396.900000 37.970000 50.000000

Create $X$ and $y$¶

In [5]:
X_full=df.drop('medv', axis=1)
y_full= df['medv']

n_samples = X_full.shape[0]
n_features = X_full.shape[1]
print(n_samples, n_features)

506 13
In [6]:
X_full.head()
Out[6]:
crim zn indus chas nox rm age dis rad tax ptratio b lstat
0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
1 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
2 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
3 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
4 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33

Look for NA values in the dataset¶

In [7]:
X_full.isna().sum()
Out[7]:
crim       0
zn         0
indus      0
chas       0
nox        0
rm         0
age        0
dis        0
rad        0
tax        0
ptratio    0
b          0
lstat      0
dtype: int64

There is none

Step 2: Exploratory Data Analysis

¶

Quantity to predict= price (target or $y$)¶

Before the regression, let us inspect the features and their distributions.

In [8]:
y_full.shape
Out[8]:
(506,)
In [9]:
sns.set(rc={'figure.figsize':(6,4)})
plt.hist(y_full, bins=30)
plt.xlabel("House prices in $1000", size=15)
plt.ylabel('count', size=15)
plt.title('Distribution of median price in each neighborhood', size=20)
plt.show()
No description has been provided for this image

Features ($X$) used for prediction¶

In [10]:
X_full.shape
Out[10]:
(506, 13)

Distributions¶

Histogram plots to look at the distribution

In [11]:
X_full.hist(bins=50, figsize=(15,10))
plt.show()
No description has been provided for this image

Correlations¶

Boston Correlation Heatmap Example with Seaborn

The seaborn package offers a heatmap that will allow a two-dimensional graphical representation of the Boston data. The heatmap will represent the individual values that are contained in a matrix are represented as colors.

In [12]:
import pandas as pd
import matplotlib.pyplot as plt
correlation_matrix = X_full.corr().round(2)
sns.heatmap(correlation_matrix) #annot=True
plt.show()
No description has been provided for this image

Check for multicolinearity¶

An important point in selecting features for a linear regression model is to check for multicolinearity.

The features RAD, TAX have a correlation of 0.91. These feature pairs are strongly correlated to each other. This can affect the model.

Same goes for the features DIS and AGE which have a correlation of -0.75.

Correlation plots¶

In [13]:
from pandas.plotting import scatter_matrix
scatter_matrix(X_full, figsize=(12, 8))
Out[13]:
array([[<Axes: xlabel='crim', ylabel='crim'>,
        <Axes: xlabel='zn', ylabel='crim'>,
        <Axes: xlabel='indus', ylabel='crim'>,
        <Axes: xlabel='chas', ylabel='crim'>,
        <Axes: xlabel='nox', ylabel='crim'>,
        <Axes: xlabel='rm', ylabel='crim'>,
        <Axes: xlabel='age', ylabel='crim'>,
        <Axes: xlabel='dis', ylabel='crim'>,
        <Axes: xlabel='rad', ylabel='crim'>,
        <Axes: xlabel='tax', ylabel='crim'>,
        <Axes: xlabel='ptratio', ylabel='crim'>,
        <Axes: xlabel='b', ylabel='crim'>,
        <Axes: xlabel='lstat', ylabel='crim'>],
       [<Axes: xlabel='crim', ylabel='zn'>,
        <Axes: xlabel='zn', ylabel='zn'>,
        <Axes: xlabel='indus', ylabel='zn'>,
        <Axes: xlabel='chas', ylabel='zn'>,
        <Axes: xlabel='nox', ylabel='zn'>,
        <Axes: xlabel='rm', ylabel='zn'>,
        <Axes: xlabel='age', ylabel='zn'>,
        <Axes: xlabel='dis', ylabel='zn'>,
        <Axes: xlabel='rad', ylabel='zn'>,
        <Axes: xlabel='tax', ylabel='zn'>,
        <Axes: xlabel='ptratio', ylabel='zn'>,
        <Axes: xlabel='b', ylabel='zn'>,
        <Axes: xlabel='lstat', ylabel='zn'>],
       [<Axes: xlabel='crim', ylabel='indus'>,
        <Axes: xlabel='zn', ylabel='indus'>,
        <Axes: xlabel='indus', ylabel='indus'>,
        <Axes: xlabel='chas', ylabel='indus'>,
        <Axes: xlabel='nox', ylabel='indus'>,
        <Axes: xlabel='rm', ylabel='indus'>,
        <Axes: xlabel='age', ylabel='indus'>,
        <Axes: xlabel='dis', ylabel='indus'>,
        <Axes: xlabel='rad', ylabel='indus'>,
        <Axes: xlabel='tax', ylabel='indus'>,
        <Axes: xlabel='ptratio', ylabel='indus'>,
        <Axes: xlabel='b', ylabel='indus'>,
        <Axes: xlabel='lstat', ylabel='indus'>],
       [<Axes: xlabel='crim', ylabel='chas'>,
        <Axes: xlabel='zn', ylabel='chas'>,
        <Axes: xlabel='indus', ylabel='chas'>,
        <Axes: xlabel='chas', ylabel='chas'>,
        <Axes: xlabel='nox', ylabel='chas'>,
        <Axes: xlabel='rm', ylabel='chas'>,
        <Axes: xlabel='age', ylabel='chas'>,
        <Axes: xlabel='dis', ylabel='chas'>,
        <Axes: xlabel='rad', ylabel='chas'>,
        <Axes: xlabel='tax', ylabel='chas'>,
        <Axes: xlabel='ptratio', ylabel='chas'>,
        <Axes: xlabel='b', ylabel='chas'>,
        <Axes: xlabel='lstat', ylabel='chas'>],
       [<Axes: xlabel='crim', ylabel='nox'>,
        <Axes: xlabel='zn', ylabel='nox'>,
        <Axes: xlabel='indus', ylabel='nox'>,
        <Axes: xlabel='chas', ylabel='nox'>,
        <Axes: xlabel='nox', ylabel='nox'>,
        <Axes: xlabel='rm', ylabel='nox'>,
        <Axes: xlabel='age', ylabel='nox'>,
        <Axes: xlabel='dis', ylabel='nox'>,
        <Axes: xlabel='rad', ylabel='nox'>,
        <Axes: xlabel='tax', ylabel='nox'>,
        <Axes: xlabel='ptratio', ylabel='nox'>,
        <Axes: xlabel='b', ylabel='nox'>,
        <Axes: xlabel='lstat', ylabel='nox'>],
       [<Axes: xlabel='crim', ylabel='rm'>,
        <Axes: xlabel='zn', ylabel='rm'>,
        <Axes: xlabel='indus', ylabel='rm'>,
        <Axes: xlabel='chas', ylabel='rm'>,
        <Axes: xlabel='nox', ylabel='rm'>,
        <Axes: xlabel='rm', ylabel='rm'>,
        <Axes: xlabel='age', ylabel='rm'>,
        <Axes: xlabel='dis', ylabel='rm'>,
        <Axes: xlabel='rad', ylabel='rm'>,
        <Axes: xlabel='tax', ylabel='rm'>,
        <Axes: xlabel='ptratio', ylabel='rm'>,
        <Axes: xlabel='b', ylabel='rm'>,
        <Axes: xlabel='lstat', ylabel='rm'>],
       [<Axes: xlabel='crim', ylabel='age'>,
        <Axes: xlabel='zn', ylabel='age'>,
        <Axes: xlabel='indus', ylabel='age'>,
        <Axes: xlabel='chas', ylabel='age'>,
        <Axes: xlabel='nox', ylabel='age'>,
        <Axes: xlabel='rm', ylabel='age'>,
        <Axes: xlabel='age', ylabel='age'>,
        <Axes: xlabel='dis', ylabel='age'>,
        <Axes: xlabel='rad', ylabel='age'>,
        <Axes: xlabel='tax', ylabel='age'>,
        <Axes: xlabel='ptratio', ylabel='age'>,
        <Axes: xlabel='b', ylabel='age'>,
        <Axes: xlabel='lstat', ylabel='age'>],
       [<Axes: xlabel='crim', ylabel='dis'>,
        <Axes: xlabel='zn', ylabel='dis'>,
        <Axes: xlabel='indus', ylabel='dis'>,
        <Axes: xlabel='chas', ylabel='dis'>,
        <Axes: xlabel='nox', ylabel='dis'>,
        <Axes: xlabel='rm', ylabel='dis'>,
        <Axes: xlabel='age', ylabel='dis'>,
        <Axes: xlabel='dis', ylabel='dis'>,
        <Axes: xlabel='rad', ylabel='dis'>,
        <Axes: xlabel='tax', ylabel='dis'>,
        <Axes: xlabel='ptratio', ylabel='dis'>,
        <Axes: xlabel='b', ylabel='dis'>,
        <Axes: xlabel='lstat', ylabel='dis'>],
       [<Axes: xlabel='crim', ylabel='rad'>,
        <Axes: xlabel='zn', ylabel='rad'>,
        <Axes: xlabel='indus', ylabel='rad'>,
        <Axes: xlabel='chas', ylabel='rad'>,
        <Axes: xlabel='nox', ylabel='rad'>,
        <Axes: xlabel='rm', ylabel='rad'>,
        <Axes: xlabel='age', ylabel='rad'>,
        <Axes: xlabel='dis', ylabel='rad'>,
        <Axes: xlabel='rad', ylabel='rad'>,
        <Axes: xlabel='tax', ylabel='rad'>,
        <Axes: xlabel='ptratio', ylabel='rad'>,
        <Axes: xlabel='b', ylabel='rad'>,
        <Axes: xlabel='lstat', ylabel='rad'>],
       [<Axes: xlabel='crim', ylabel='tax'>,
        <Axes: xlabel='zn', ylabel='tax'>,
        <Axes: xlabel='indus', ylabel='tax'>,
        <Axes: xlabel='chas', ylabel='tax'>,
        <Axes: xlabel='nox', ylabel='tax'>,
        <Axes: xlabel='rm', ylabel='tax'>,
        <Axes: xlabel='age', ylabel='tax'>,
        <Axes: xlabel='dis', ylabel='tax'>,
        <Axes: xlabel='rad', ylabel='tax'>,
        <Axes: xlabel='tax', ylabel='tax'>,
        <Axes: xlabel='ptratio', ylabel='tax'>,
        <Axes: xlabel='b', ylabel='tax'>,
        <Axes: xlabel='lstat', ylabel='tax'>],
       [<Axes: xlabel='crim', ylabel='ptratio'>,
        <Axes: xlabel='zn', ylabel='ptratio'>,
        <Axes: xlabel='indus', ylabel='ptratio'>,
        <Axes: xlabel='chas', ylabel='ptratio'>,
        <Axes: xlabel='nox', ylabel='ptratio'>,
        <Axes: xlabel='rm', ylabel='ptratio'>,
        <Axes: xlabel='age', ylabel='ptratio'>,
        <Axes: xlabel='dis', ylabel='ptratio'>,
        <Axes: xlabel='rad', ylabel='ptratio'>,
        <Axes: xlabel='tax', ylabel='ptratio'>,
        <Axes: xlabel='ptratio', ylabel='ptratio'>,
        <Axes: xlabel='b', ylabel='ptratio'>,
        <Axes: xlabel='lstat', ylabel='ptratio'>],
       [<Axes: xlabel='crim', ylabel='b'>,
        <Axes: xlabel='zn', ylabel='b'>,
        <Axes: xlabel='indus', ylabel='b'>,
        <Axes: xlabel='chas', ylabel='b'>,
        <Axes: xlabel='nox', ylabel='b'>,
        <Axes: xlabel='rm', ylabel='b'>,
        <Axes: xlabel='age', ylabel='b'>,
        <Axes: xlabel='dis', ylabel='b'>,
        <Axes: xlabel='rad', ylabel='b'>,
        <Axes: xlabel='tax', ylabel='b'>,
        <Axes: xlabel='ptratio', ylabel='b'>,
        <Axes: xlabel='b', ylabel='b'>,
        <Axes: xlabel='lstat', ylabel='b'>],
       [<Axes: xlabel='crim', ylabel='lstat'>,
        <Axes: xlabel='zn', ylabel='lstat'>,
        <Axes: xlabel='indus', ylabel='lstat'>,
        <Axes: xlabel='chas', ylabel='lstat'>,
        <Axes: xlabel='nox', ylabel='lstat'>,
        <Axes: xlabel='rm', ylabel='lstat'>,
        <Axes: xlabel='age', ylabel='lstat'>,
        <Axes: xlabel='dis', ylabel='lstat'>,
        <Axes: xlabel='rad', ylabel='lstat'>,
        <Axes: xlabel='tax', ylabel='lstat'>,
        <Axes: xlabel='ptratio', ylabel='lstat'>,
        <Axes: xlabel='b', ylabel='lstat'>,
        <Axes: xlabel='lstat', ylabel='lstat'>]], dtype=object)
No description has been provided for this image

Scatter plot relative to the target (price)¶

In [14]:
(X_full.columns)
Out[14]:
Index(['crim', 'zn', 'indus', 'chas', 'nox', 'rm', 'age', 'dis', 'rad', 'tax',
       'ptratio', 'b', 'lstat'],
      dtype='object')
In [15]:
fig, axs= plt.subplots(3, 5, figsize=(20, 12))
i=0
for ax in axs.flat:
    if i<len(X_full.columns):
        feature_name = X_full.columns[i]  
        ax.scatter(X_full[feature_name], y_full, alpha=0.1)
        ax.set(xlabel=feature_name, ylabel='Price')
        i=i+1
No description has been provided for this image

What can we say ?¶

  • The prices increase as the value of RM increases linearly. There are few outliers and the data seems to be capped at 50.

  • The prices tend to decrease with an increase in LSTAT. Though it doesn’t look to be following exactly a linear line.

Linear Regression as a predictive model¶

Model building¶

  • Deciding about the predictors to include in the model and their functional form.

  • We have strong computers, cloud, etc - why could not we try out all possible models and pick the best one?

    • Too many models possible!

  • 2 methods to build models:

    1. By hand -- mix domain knowledge and statistics
    2. By Smart algorithms $=$ machine learning

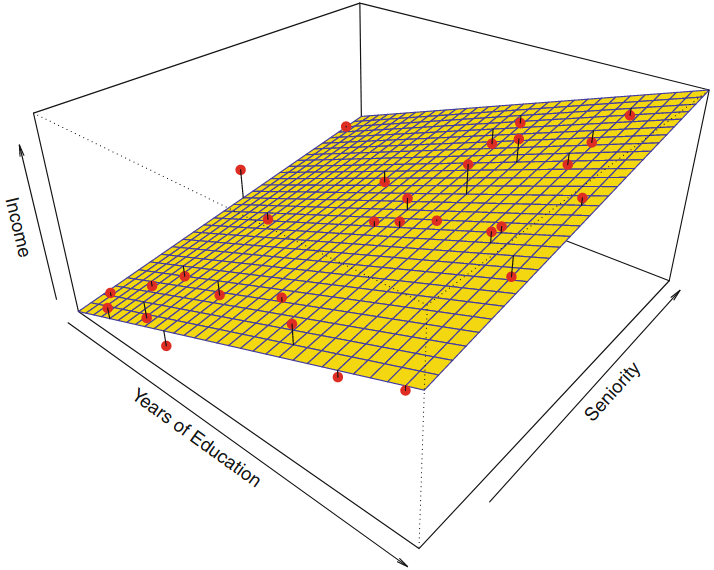
Linear Regression¶

$$Y=\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p + \epsilon $$

$=$ one of the simplest algorithms for doing supervised learning

A good starting point before studying more complex learning methods

Interpretation of $\beta_j$ = the average effect on $Y$ of a unit increase in $X_j$ holding all other predictors fixed

Linear estimate¶

No description has been provided for this image

Notes: the true $f$ has some curvature that is not captured in the linear fit

Linear Models: pros and cons¶

  • Pros:

    • Interpretability
    • Good predictive performance
    • Accuracy measures for
      • coefficient estimates (standard errors and confidence intervals)
      • the model

  • Cons:

    • When $p>n$
    • Tend to over-fit training data.
    • Cannot handle multicollinearity.

Core ML concepts¶

Undefittin vs. Overfitting: Split the Sample Between Three Economists¶

Underffiting: High Bias, Low Variance¶

The model: unconditional mean $$Y_i = \beta_0+\varepsilon_i$$

No description has been provided for this image

Overfitting: Low Bias, High Variance¶

The model: high-degree polynomial

$$Y_i = \beta_0+\sum_{j=1}^{\lambda}\beta_jX_i^{\lambda}+\varepsilon_i$$

No description has been provided for this image

"Justfitting": Bias and Variance are Just Right¶

The model: linear regression

$$Y_i = \beta_0+\beta_1 X_i + \varepsilon_i$$

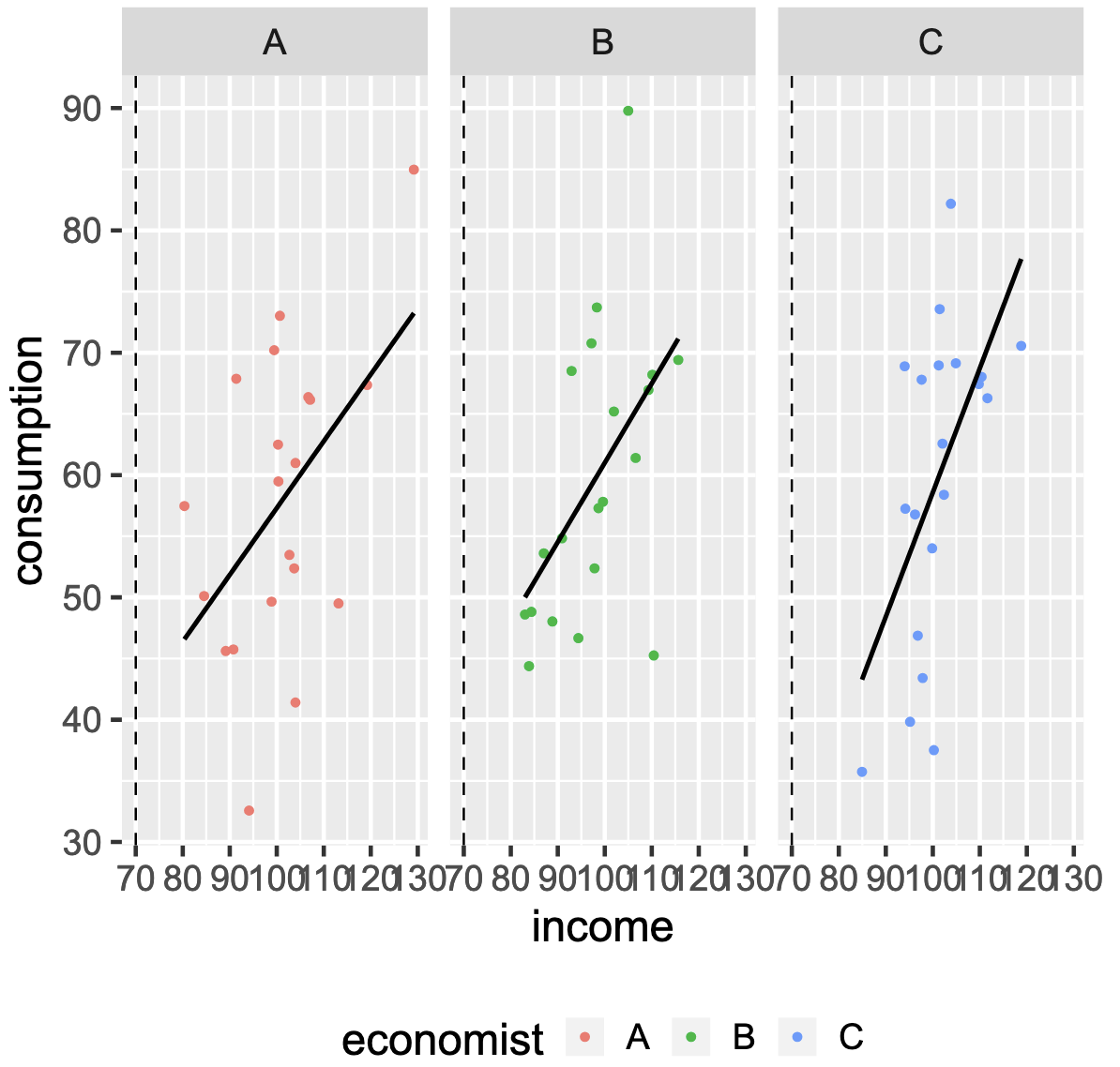
No description has been provided for this image

The Typical Bias-Variance Trade-off in ML¶

Typically, ML models strive to find levels of bias and variance that are "just right":

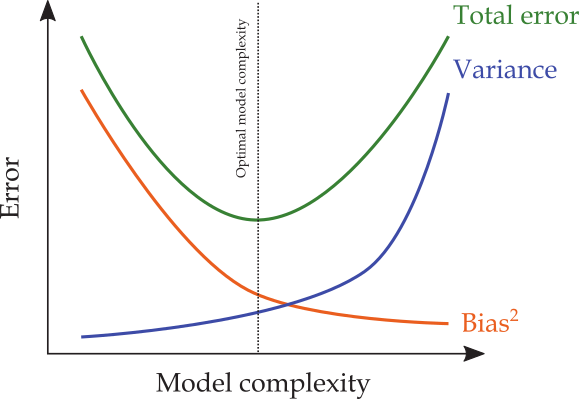
No description has been provided for this image

When is the Bias-Variance Trade-off Important?¶

In low-dimensional settings ( $n\gg p$ )

  • overfitting is highly unlikely
  • training MSE closely approximates test MSE
  • conventional tools (e.g., OLS) will perform well on a test set

INTUITION: As $n\rightarrow\infty$, insignificant terms will converge to their true value (zero).

In high-dimensional settings ( $n\ll p$ )

  • overfitting is highly likely
  • training MSE poorly approximates test MSE
  • conventional tools tend to overfit

$n\ll p$ is prevalent in big-data

Measuring the Performance of a Model using Mean Squared Error (MSE)¶

$$MSE= \frac{1}{n} \sum_{i=1}^n (y_i - \hat f(x_i))^2$$

  • Regression setting: the mean squared error is a metric of how well a model fits the data.

MSE will be small if the predicted responses are very close to the true responses,and will be large if for some of the observations, the predicted and true responses differ substantially

= Aggregated measure of the errors

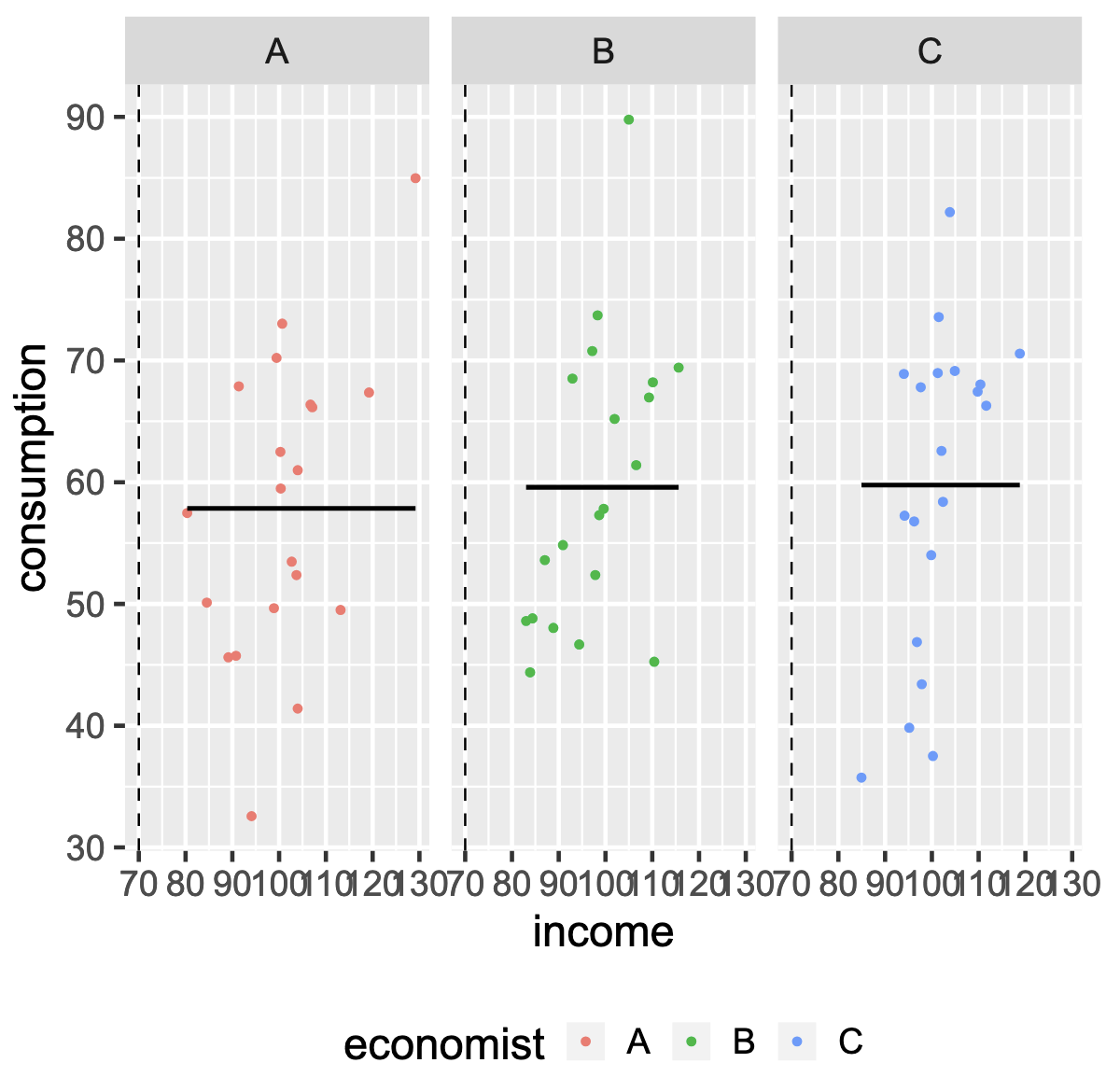
Avoiding Overfitting: train/test split¶

In [ ]:
<table>
    <tr>
        <td>3 simulated models</td>
        <td><span style="color: grey;">train set MSE</span> and <span style="color: red;">test set MSE</span></td>
    </tr>
</table>
In [ ]:
%%HTML
<div style="text-align: center;"> style="text-align: center;">
    <table>
            <td>3 simulated models</td>
            <td> Flexibility:<span style="color: grey;">train set MSE</span> and <span style="color: red;">test set MSE</span></td>
        </tr>
    </table>
</div>

Training MSE, test MSE and model flexibility¶

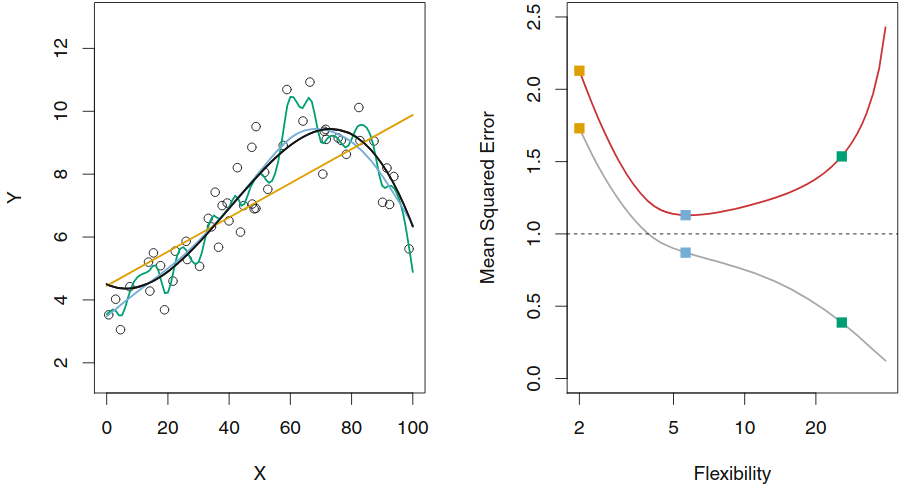
No description has been provided for this image
3 simulated models and DGP in black Flexibility:train set MSE and test set MSE

Increasing model flexibility tends to decrease training MSE but will eventually increase test MSE

  • Left:Data simulated from $f$, shown in black.

  • Three estimates of $f$ are shown:

    • the linear regression line (orange curve),
    • and two smoothing splinefits (blue and green curves).

  • Right:Training MSE (grey curve), test MSE (red curve), and minimum possible test MSE over all methods (dashed line).

  • Squares represent the training and test MSEs for the three fits shown in the left-hand panel.

  • we observe a monotone decrease in the training MSE and a U-shape in the test MSE

Overfitting¶

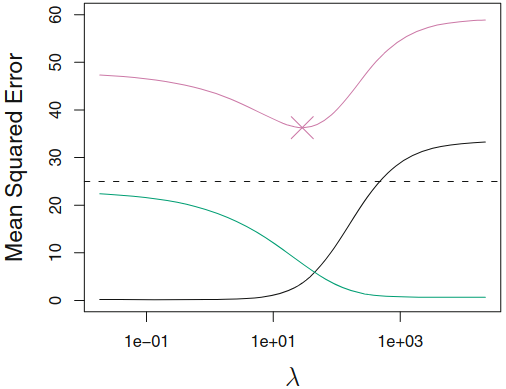
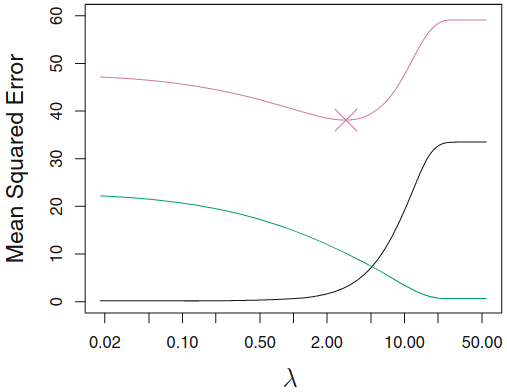
  • As model flexibility increases, training MSE will decrease, but the test MSE may not.

  • When a given method yields a small training MSE but a large test MSE, we are said to be overfitting the data.

  • (We almost always expect the training MSE to be smaller than the test MSE)

  • Estimating test MSE is important, but requires training data...

Regularization methods¶

Context: Generalization of the Linear Models¶

  • Regularized fitting: ridge regression and lasso

  • Non-linearity: nearest neighbor methods

  • Interactions: Tree-based methods, random forests and boosting

Why Regularization?¶

  • Key question: which features to enter into model, how to select?

    • There is room for an automatic selection process.

  • Solution against overfitting

  • Allow High-Dimensional Predictors

    • $p>>n$: OLS no longer has a unique solution
    • $x_i$ "high-dimensional" i.e. very many regressors
    • pixels on a picture

Notes: Corollary of regularization:

  • Prediction Accuracy:especially when $p > n$, to control the variance

Adding a Regularization Term to the Loss Function $L(.)$¶

$$ \hat \beta =arg min_\beta \frac{1}{n} \sum_{i=1}^n L(h(x_i, \beta), y_i) +\lambda R(\beta) $$

  • $R(\beta)$ = regularization function

    • $R(\beta)=\sum_{i=1}^n p(\beta_i)$ for $p(.)$ the penalty function
    • measures the expressiveness of the model

  • As the number of features grows, linear models become more expressive.

  • $\lambda$ is a hyperparameter where higher values increase regularization

Notation: Norms¶

Suppose $\boldsymbol{\beta}$ is a $p\times 1$ vector with typical element $\beta_i$.

  • The $\ell_0$-norm is defined as $\lVert\boldsymbol{\beta}\rVert_0 = \sum_{j=1}^p \boldsymbol{1}\\{\beta_j \neq 0\\}$,

    • i.e., the number of non-zero elements in $\boldsymbol{\beta}$.

  • The $\ell_1$-norm is defined as $\lVert\boldsymbol{\beta}\rVert_1=\sum_{j=1}^{p}|\beta_j|$.

  • The $\ell_2$-norm is defined as $\lVert\boldsymbol{\beta}\rVert_2=\left(\sum_{j=1}^{p}|\beta_j|^2\right)^{\frac{1}{2}}$

    • i.e., Euclidean norm.

Commonly used penalty functions¶

Regularization problem:

$$\underset{\beta_{0}, \beta}{\operatorname{min}} \sum_{i=1}^{N}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} x_{i j} \beta_{j}\right)^{2}+\lambda R(\beta)$$

Method $R(\boldsymbol{\beta})$
OLS 0
Subset selection $\lVert\boldsymbol{\beta}\rVert_0$
Lasso $\lVert\boldsymbol{\beta}\rVert_1$
Ridge $\lVert\boldsymbol{\beta}\rVert_2^2$
Elastic Net $\alpha\lVert\boldsymbol{\beta}\rVert_1 + (1-\alpha)\lVert\boldsymbol{\beta}\rVert_2^2$

Prerequisite: centering and scaling¶

In what follows, we assume that each feature is centered and scaled to have mean zero and unit variance, as follows:

$$\frac{x_{ij} - \widehat\mu_i}{\widehat\sigma_{i}}, \qquad\text{for }j=1,2, \ldots, p$$

where $\widehat\mu_i$ and $\widehat\sigma_i$ are the estimated mean and standard deviation of $x_i$ estimated over the training set.

Remark: This is not important when using OLS (why?)

Ridge Regression¶

$$\min_{\beta} \sum_{i=1}^n \left(y_i - \beta_{0}-\sum_{j=1}^{p} x_{i j} \beta_{j} \right)^2 + \lambda \sum_{j=1}^p \beta_j^2 $$

Where

  • $\lambda > 0$ = penalty parameter
  • covariates can be high-dimensionnal $p>>N$

Trade-off, from the minimization of the sum of

  1. RSS
  2. shrinkage penalty: decreases with $\beta_j$

$\rightarrow$ relative importance given by $\lambda$

  • The tuning parameter $\lambda$ serves to control the relative impact of these two terms on the regression coefficient estimates.
  • When $\lambda=0$, the penalty term has no effect, and ridge regression will produce the least squares estimates
  • when $\lambda \rightarrow \infty$ : penalty grows and coefficient estimates approach zero

Ridge Regression: shrinkage to $0$¶

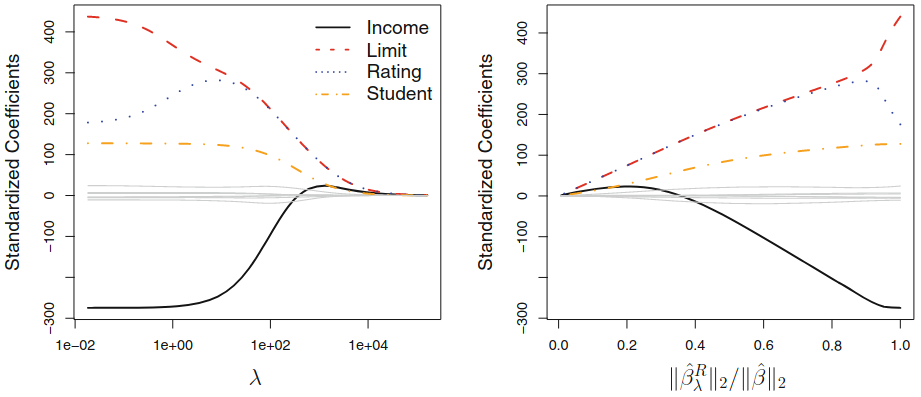
No description has been provided for this image

Ridge: Variance-Bias Trade-Off¶

No description has been provided for this image

Squared bias (black), Variance and test MSE

  • As $\lambda$ increases, the flexibility of the ridge regression fit decreases, leading to decreased variance but increased bias
  • Up to 10, the variance decreases rapidly, with very little increase in bias
  • Beyond this point, the decrease in variance due to increasing $\lambda$ slows, and the shrinkage on the coefficients causes them to be significantly underestimated
  • Recall that the test MSE (purple), is a function of the variance plus the squared bias.

Ridge vs. Linear Models¶

  • when outcome and predictors are close to having a linear relationship, the OLS will have low bias but potentially high variance
    • small change in the training data $\rightarrow$ large change in the estimates
    • worse with $p$ close tp $n$
    • if $p>n$, OLS do not have a unique solution

$\rightarrow$ ridge regression works best in situations where the least squares estimates have high variance

LASSO (Least Absolute Shrinkage and Selection Operator)¶

LASSO proposes a method to build a model which just includes the most important predictors.

Modifies the way regression coefficients are estimated by adding a penalty term for too many coefficients

Notes: Ridge: the penalty shinks coefficients toward $0$ but not exactly to $0$

This may not be a problem for prediction accuracy, but it can create a challenge in model interpretation when $p$ is quite large

Lasso¶

$$ \hat \beta =arg min_\beta \frac{1}{n} \sum_{i=1}^n \left( y_i -(\beta_0 + \sum_{j=1}^k\beta_jx_{ij})\right)^2 +\lambda \sum_{j=1}^k |\beta_j| $$

  • $R(\beta)= \sum_{j=1}^k |\beta_j|=$ regularization function with a $\ell_1$-norm penalty function

  • $\lambda$ is a hyperparameter (or tunning) where higher values increase regularization

Notes:

  • Lasso automatically performs feature selection and outputs a sparse model.

Lasso Coefficients¶

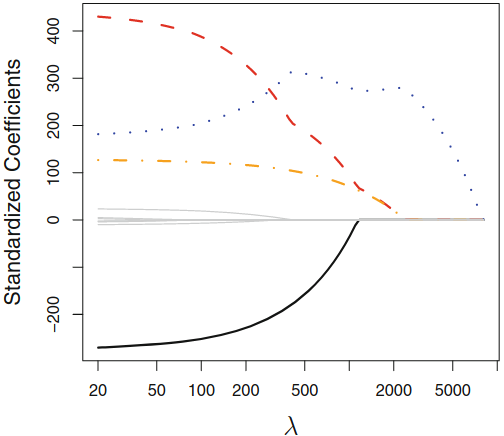
No description has been provided for this image
  • When $\lambda=0$: the lasso simply gives the least squares fit
  • when $\lambda$ becomes sufficiently large, the lasso gives the null model in which all coefficient estimates equal 0.
  • in between these two extremes, the ridge regression and lasso models are quite different from each other

Lasso: Variance-Bias Trade-Off¶

No description has been provided for this image

Squared bias (black), variance (green), [test] MSE (red)

Constrained Regression¶

The minimization problem can be written as follow:

$$ \sum_{i=1}^n(y_i-x_i'\beta)^2 \textrm{ s.t. } \sum_{j=1}^p p(\beta_j) \leq s,$$

Where

  • Ridge: $\sum_{j=1}^p \beta_j^2 <s $ $\rightarrow$ equation of a circle
  • Lasso: $\sum_{j=1}^p |\beta_j| <s $ $\rightarrow$ equation of a diamond

Notes:

  • Lasso: we try to find the set of coefficient estimates that lead to the smallest RSS, subject to the constraint that there is a budgets for how large $\sum_{j=1}^p |\beta_j|$ can be.
  • if $s$ is extremely large, it is not very restrictive and the least square solution falls within the budget

Constraint Regions: Lasso vs. ridge¶

Contours of the error and constraint functions for lasso (left) and ridge (right).

  • The solid blue areas are the constraint regions, $\beta_{1}^{2}+\beta_{2}^{2} \leq \lambda,$ and $|\beta_{1}|+|\beta_{2}| \leq \lambda$
  • the red ellipses are the contours of the RSS and $\widehat\beta$ is the OLS estimator.
Lasso Ridge
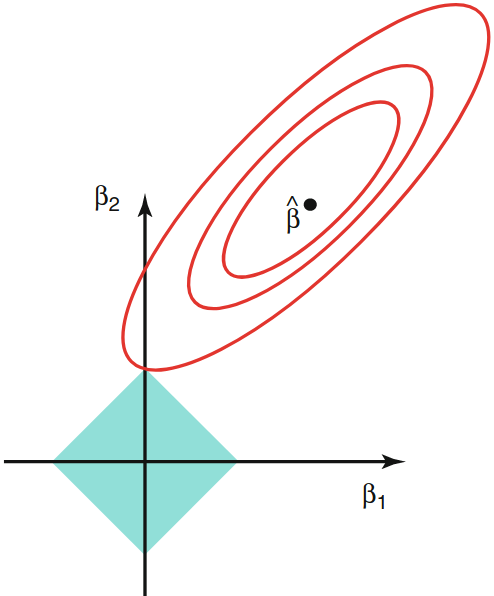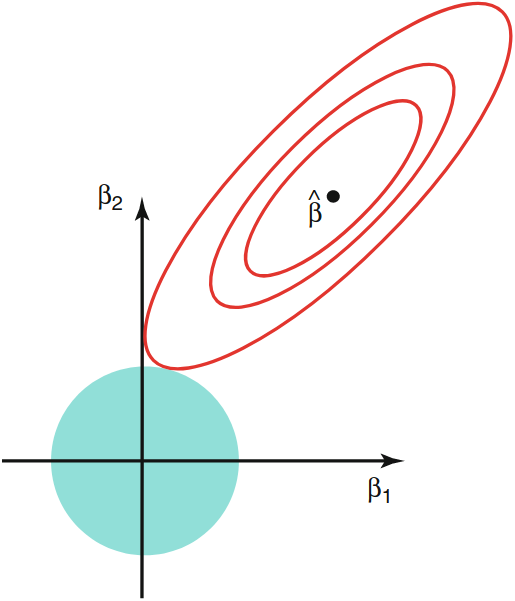No description has been provided for this image No description has been provided for this image
  • Why is it that the lasso, unlike ridge regression, results in coefficient estimates that are exactly equal to zero?
  • diamonds & circle represent the ridge & lasso constraint regions
  • the red ellipses are the contours of the RSS (for different levels of RSS): regions centered around $\beta$ of constant value of RSS
  • $\hat \beta$ is the least square estimate
  • the lasso constraint has corners at each of the axes, and so the ellipse will often intersect the constraint region at an axis $\rightarrow$ When this occurs, one of the coefficients will equal zero.

Elastic Net = Lasso + Ridge¶

$$ MSE(\beta)+\lambda_1 \sum_{j=1}^p |\beta_j| +\lambda_2 \sum_{j=1}^p \beta_j^2$$

$\lambda_1$, $\lambda_2$ $=$ strength of $\ell_1$-norm (Lasso) penalty and $\ell_2^2$-norm (Ridge) penalty

Selecting Elastic Net Hyperparameters¶

  • Elastic net hyperparameters should be selected to optimize out-of-sample fit (measured by mean squared error or MSE).

  • “Grid search”

    • scans over the hyperparameter space ($\lambda_1 \geq 0, \lambda_2\geq 0$),
    • computes out-of-sample MSE for all pairs $(\lambda_1, \lambda_2)$ ,
    • selects the MSE-minimizing model.

Feature Engineering¶

2 extensions of the Linear Model¶

Going further model's assumptions:

  • the additive: the effect of changes in a predictor $X_j$ on the response $Y$ is independent of the values of the other predictors

  • linearity: the change in the response $Y$ due to a one-unit change in $X_j$ is constant

Non Linearity¶

  • Include transformed versions of the predictors in the model

$\Rightarrow$ Including polynomials in $X$ may provide a better fit

Scikit-Learn Design Overview¶

Transformer (preprocessor): An object that transforms a data set.¶

  • e.g. preprocessing.StandardScaler
  • Transformation is performed by the transform() method.

Estimator: an object that can estimate parameters¶

  • e.g. linear_models.LinearRegression
  • Estimation performed by fit() method
  • Exogenous parameters (provided by the researcher) are called hyperparameters
  • The convenience method fit_transform() both fits an estimator and returns the transformed input data set.

Predictor: An object that forms a prediction from an input data set.¶

  • e.g. LinearRegression, after training
  • The predict() method forms the predictions.
  • It also has a score() method that measures the quality of the predictions given a test set.

Step 3: set, train and evaluate the model

¶

Data cleaning¶

The missing features should be either:

  1. dropped
  2. imputed to some value (zero, the mean, the median...)

Drop the observations with price >=50 (because of the right censure)

In [16]:
mask=y_full<50

y_full=y_full[mask==True]
X_full=X_full[mask==True]

Prepare Training and Test Sets using train_test_split¶

Pure ramdomness of the sampling method

In [17]:
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_full, y_full,test_size=0.2, random_state=1)

print("train data", X_train.shape, y_train.shape)
print("test data", X_test.shape,  y_test.shape)

train data (392, 13) (392,)
test data (98, 13) (98,)

Feature Scaling¶

Most common scaling methods:

  • standardization= normalization by substracting the mean and dividing by the standard deviation (values are not bounded)

$x_1^{scaled} = \frac{x^1 - \bar x_1 }{sd(x^1)}$

  • Min-max scaling= normalization by substracting the minimum and dividing by the maximum (values between 0 and 1)
In [18]:
from sklearn.preprocessing import StandardScaler, MinMaxScaler

scaler = StandardScaler().fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

Select and Train a Model¶

Regression algorithm (we consider firs the LinearRegression, more algorithms will be discussed later):

In [19]:
# our first machine learning model
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg
Out[19]:
LinearRegression()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
In [20]:
lin_reg.fit(X_train_scaled, y_train)
Out[20]:
LinearRegression()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
In [21]:
print("R-squared for training dataset:{}".
      format(np.round(lin_reg.score(X_train_scaled, y_train), 2)))

R-squared for training dataset:0.79
In [22]:
print("R-squared for test dataset:{}".
      format(np.round(lin_reg.score(X_test_scaled, y_test), 2)))

R-squared for test dataset:0.73

Note: $R^2 =$ the proportion of variance (of $y$) that has been explained by the independent variables in the model.

Coefficients of the linear regression¶

In [23]:
lin_reg.coef_
Out[23]:
array([-0.82250959,  0.96267645, -0.54388693,  0.187684  , -1.50325117,
        2.15830284, -0.54795352, -2.78522878,  2.16616351, -2.21708013,
       -1.8582422 ,  0.71805978, -2.70105292])
In [25]:
print('The coefficients of the features from the linear model:')
print(dict(zip(features, [round(x, 2) for x in lin_reg.coef_])))

The coefficients of the features from the linear model:
{'crim': -0.82, 'zn': 0.96, 'indus': -0.54, 'chas': 0.19, 'nox': -1.5, 'rm': 2.16, 'age': -0.55, 'dis': -2.79, 'rad': 2.17, 'tax': -2.22, 'ptratio': -1.86, 'b': 0.72, 'lstat': -2.7}

Choose the best model with cross-validation¶

k-fold Cross-validation¶

Split the training set into $k$ roughly equal-sized parts ( $k=5$ in this example):

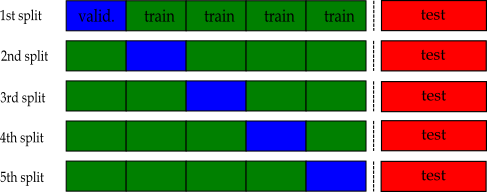
No description has been provided for this image

Approximate the test-MSE using the mean of $k$ split-MSEs

$$\text{CV-MSE} = \frac{1}{k}\sum_{j=1}^{k}\text{MSE}_j$$

Step 4: Cross-validation

¶

K-Fold CV¶

In [26]:
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn.model_selection import KFold
In [27]:
# Perform 5-fold cross validation
scores = cross_val_score(lin_reg, X_train_scaled, y_train, 
                         scoring="neg_mean_squared_error", # evaluation metrics
                         cv=5)
scores
Out[27]:
array([ -7.74021081, -15.46731828, -14.72344763, -17.14433289,
       -18.96092531])
In [28]:
# the other way of doing the same thing (more explicit)

# create a KFold object with 5 splits 
folds = KFold(n_splits = 5, shuffle = True, random_state = 100)
scores = cross_val_score(lin_reg, X_train_scaled, y_train, scoring='neg_mean_squared_error', cv=folds)
scores
Out[28]:
array([-18.32023985, -11.84760498, -17.04867667, -16.44238641,
       -10.9874587 ])

Hyperparameter Tuning Using Grid Search Cross-Validation¶

A common use of cross-validation is for tuning hyperparameters of a model. The most common technique is what is called grid search cross-validation.

In [29]:
# 1. create a cross-validation scheme
from sklearn.model_selection import KFold
kfold = KFold(n_splits=10,random_state=2, shuffle=True) 
kfold
Out[29]:
KFold(n_splits=10, random_state=2, shuffle=True)
In [30]:
# 2. specify range of hyperparameters to tune
param_grid = [
  {'alpha': [0.0001, 0.001, 0.01, 0.1 ,1, 10],
      'l1_ratio':[.1,.5,.9,1]}   
]
In [31]:
from sklearn.model_selection import GridSearchCV
In [32]:
# 3. perform grid search
# 3.1 specify model
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet()
In [33]:
# 3.2 call GridSearchCV()

# train across 5 folds, that's a total of (12+6)*5=90 rounds of training 
model_cv = GridSearchCV(elastic_net, param_grid, cv=kfold,
                           scoring='neg_mean_squared_error',
                           return_train_score=True)
model_cv
Out[33]:
GridSearchCV(cv=KFold(n_splits=10, random_state=2, shuffle=True),
             estimator=ElasticNet(),
             param_grid=[{'alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10],
                          'l1_ratio': [0.1, 0.5, 0.9, 1]}],
             return_train_score=True, scoring='neg_mean_squared_error')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=KFold(n_splits=10, random_state=2, shuffle=True),
             estimator=ElasticNet(),
             param_grid=[{'alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10],
                          'l1_ratio': [0.1, 0.5, 0.9, 1]}],
             return_train_score=True, scoring='neg_mean_squared_error')
ElasticNet()
ElasticNet()
In [34]:
# fit the model
model_cv.fit(X_train_scaled, y_train)
Out[34]:
GridSearchCV(cv=KFold(n_splits=10, random_state=2, shuffle=True),
             estimator=ElasticNet(),
             param_grid=[{'alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10],
                          'l1_ratio': [0.1, 0.5, 0.9, 1]}],
             return_train_score=True, scoring='neg_mean_squared_error')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=KFold(n_splits=10, random_state=2, shuffle=True),
             estimator=ElasticNet(),
             param_grid=[{'alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10],
                          'l1_ratio': [0.1, 0.5, 0.9, 1]}],
             return_train_score=True, scoring='neg_mean_squared_error')
ElasticNet(alpha=0.01, l1_ratio=0.1)
ElasticNet(alpha=0.01, l1_ratio=0.1)
In [35]:
# cv results
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results.head()
Out[35]:
mean_fit_time std_fit_time mean_score_time std_score_time param_alpha param_l1_ratio params split0_test_score split1_test_score split2_test_score ... split2_train_score split3_train_score split4_train_score split5_train_score split6_train_score split7_train_score split8_train_score split9_train_score mean_train_score std_train_score
0 0.004507 0.005245 0.001400 0.002163 0.0001 0.1 {'alpha': 0.0001, 'l1_ratio': 0.1} -13.406530 -14.328648 -12.011451 ... -13.755289 -13.819750 -13.797527 -13.206681 -13.885470 -11.411172 -13.730520 -13.507182 -13.428291 0.698492
1 0.000864 0.000134 0.000324 0.000040 0.0001 0.5 {'alpha': 0.0001, 'l1_ratio': 0.5} -13.408003 -14.328863 -12.011969 ... -13.755289 -13.819749 -13.797526 -13.206680 -13.885470 -11.411172 -13.730519 -13.507181 -13.428290 0.698492
2 0.001147 0.000544 0.000569 0.000521 0.0001 0.9 {'alpha': 0.0001, 'l1_ratio': 0.9} -13.409477 -14.329080 -12.012521 ... -13.755288 -13.819749 -13.797526 -13.206680 -13.885469 -11.411171 -13.730518 -13.507181 -13.428289 0.698492
3 0.000787 0.000105 0.000324 0.000050 0.0001 1.0 {'alpha': 0.0001, 'l1_ratio': 1} -13.409844 -14.329135 -12.012652 ... -13.755288 -13.819749 -13.797525 -13.206680 -13.885469 -11.411171 -13.730518 -13.507181 -13.428289 0.698492
4 0.000756 0.000107 0.000287 0.000008 0.0010 0.1 {'alpha': 0.001, 'l1_ratio': 0.1} -13.354994 -14.323175 -11.994855 ... -13.755485 -13.819927 -13.797724 -13.206868 -13.885637 -11.411323 -13.730734 -13.507338 -13.428476 0.698504

5 rows × 32 columns

In [36]:
# plotting cv results
plt.figure(figsize=(16,6))
a= 0.01
plt.plot(cv_results.loc[cv_results['param_alpha']==a,"param_l1_ratio"], cv_results[cv_results['param_alpha']==a]["mean_test_score"])
plt.plot(cv_results.loc[cv_results['param_alpha']==a,"param_l1_ratio"], cv_results[cv_results['param_alpha']==a]["mean_train_score"])
plt.xlabel('L1 ratio')
plt.ylabel('Negative MSE')
plt.title("Optimal L1 ratio parameter for alpha={}".format(a) )   
plt.legend(['test score', 'train score'], loc='upper right')
Out[36]:
<matplotlib.legend.Legend at 0x324e73a40>
No description has been provided for this image

Step 5: Best model implementation and evaluation

¶

Now we can choose the optimal value of number of features and build a final model.

In [37]:
best_alpha = model_cv.best_params_['alpha']
best_l1_ratio = model_cv.best_params_['l1_ratio']
print("Best alpha: ", best_alpha,   "Best l1_ratio: ", best_l1_ratio)   

Best alpha:  0.01 Best l1_ratio:  0.1
In [38]:
# Fit model (to the training set) with optimal alpha and l1_ratio
elastic_net = ElasticNet(alpha=best_alpha, l1_ratio=best_l1_ratio)  
elastic_net.fit(X_train_scaled, y_train)
Out[38]:
ElasticNet(alpha=0.01, l1_ratio=0.1)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ElasticNet(alpha=0.01, l1_ratio=0.1)
In [39]:
# predict prices of X_test
y_test_pred = elastic_net.predict(X_test_scaled)
In [40]:
# Evaluate the model
from sklearn.metrics import mean_squared_error

test_mse = mean_squared_error(y_test, y_test_pred)
test_rmse = np.sqrt(test_mse)
print("RMSE on test data: ", test_rmse)

RMSE on test data:  3.8754693909725972

NOTE: the test set RMSE estimates the expected squared prediction error on unseen data given the best model.

MSE vs. $R^2$¶

MSE :

  • good for comparing regression models,
  • but the units depend on the outcome variable and
  • $\Rightarrow$ are not interpretable

Better to use $R^2$ in the test set: same ranking as MSE but it more interpretable.